『形式意味論入門』を Haskell に書き下す (後編)

この記事は以下のページに移転しました．

前編はこちら

ryota-ka.hatenablog.com

§8 発話文脈・変項割当

${\it \text{She loves him.}}$

という文を発話したとする．この文は，代名詞 ${\it \text{she}}$ と ${ \it \text{him}}$ の2つの指示対象が発話の状況から明らかなときにのみ適切である．このように，文脈に依存して意味が初めて定まる言語表現を直示 (deixis) という．指示対象を明らかにするため，次のように代名詞に指標 (index) を振ることにする．

$\it{\text{She}_{\rm 1} \text{ loves } \text{him}_{\rm 2}.}$

${\it \text{She}}$ と ${\it \text{him}}$ に $1$ と $2$ という異なる指標が割り当てられているのは，それらが相異なる外延をもつことを表している．

既に述べたように，この文の外延は ${\it \text{She}_{\rm 1}}$ および ${\it \text{him}_{\rm 2}}$ の指示対象が文脈から定まることで初めて計算することができる．このような文は自由変項*1を含んだ開いた項 (open term) として見做すことができる．このような発話に際しての状況を utterance context と呼ぶ．定訳があるかはわからないので，この記事中では発話文脈と訳すことにする．

発話文脈を形式的に扱う道具立てとして，変項割当 (variable assignment) を導入する．Heim and Kratzer では，変項割当を以下のように定義している*2．

(変項) 割当とは， $\mathbb{N}$ (自然数の集合) から $D_e$ への部分関数である．

例えば，以下の $g, g', g''$ はいずれも $\text{Model PEANUTS}$ における変項割当である．

$g = \begin{equation} \left [ \begin{aligned} &1 \mapsto \text{Snoopy} \\ &2 \mapsto \text{Woodstock} \\ \end{aligned} \right ] \end{equation}$

$g' = \begin{equation} \left [ \begin{aligned} &42 \mapsto \text{Snoopy} \\ \end{aligned} \right ] \end{equation}$

$g'' = \phi$

直示を含む項の意味計算をするには，指示対象を発話文脈に問い合わせる必要があるため，ある変項割当のもとで項の意味計算を行なう必要がある．そこで，変項割当 $g$ のもとでの項 $e$ の外延を $[\![e]\!]^g$ と表記することにする．以降 $[\![\cdot]\!]$ は $[\![\cdot]\!]^\phi$ の略記であるとする．*3

また，変項 (variable) という概念は形式的には次のように定義される*4 *5．

終端記号 $\alpha$ は， $[\![\alpha]\!]^g \neq [\![\alpha]\!]^{g'}$ となるような変項割当 $g$ および $g'$ が存在するとき，かつそのときに限り変項であるという．

変項は自由変項 (free variable) と束縛変項 (bound variable) に分類される*6が，ある項が自由変項を含む開いた項であるか，それとも自由変項を含まない閉じた項 (closed term) であるかを区別することは重要である．閉じた項の意味計算はその項の内部だけで完結する一方，開いた項の意味計算を行うためには，変項の指示対象を外部から与える必要があるからである．

§8のまとめ

発話文脈に依存して意味が初めて定まる言語表現を直示という
発話文脈を形式的に扱うために変項割当という概念を導入する
- これは $\mathbb{N}$ (自然数の集合) から $D_e$ (個体の集合) への部分関数である
直示を含む文の意味計算は変項割当をともなって行なう

§9. 新しい言語

さて，変項割当を Haskell 上で表現してみよう．変項割当は自然数の集合 $\mathbb{N}$ から個体の集合 $D_e$ への部分関数だったが，項レベルの計算で部分関数を扱いたくないので，型レベルで扱うことにする．型レベルで扱うことにより，適切でない文脈で発話がなされたことを型エラーとして検知することができる．

変項割当を導入したモチベーションは，発話文脈を形式的に扱うことであった．文脈上に存在する値を参照するような計算は，Haskell では Reader として知られている．ただし，今我々が欲しいのは単なる Reader ではなく，型レベル自然数を指定した際，その自然数に対応するような値を取ってくることのできる Reader である．このような挙動を実現するため，membership および extensible-skeleton package を用い，extensible effects を用いて対象言語を構築することにする．

自然数と個体の対応関係を表す型 index |-> entity を以下のように定義する．ここで index は型レベル自然数である，すなわち Nat 種をもつ．

import GHC.Types (Type)
import GHC.TypeNats (Nat)
import Data.Extensible.Effects (ReaderEff)
import Type.Membership (type (>:), Assoc, Lookup)

type (|->) :: Nat -> Type -> Assoc Nat (Type -> Type)
type index |-> entity = index >: ReaderEff entity

例えば 1 |-> PEANUTS という型は，指標 1 に PEANUTS 型の値が割り当てられていることを意味する．

前編で定義した Model 言語を書き換え，extensible effects に埋め込むことにする．この言語では，項が Eff ctx a という型で表現される．ただし，Eff 型は extensible-skeleton package で定義されている．ここで ctx は ctx :: [Assoc Nat (Type -> Type)] という種をもち，具体的には ctx = '[1 |-> PEANUTS, 2 |-> PEANUTS] のような型になる．e :: Eff ctx a は直観的には ctx という文脈を伴った a 型の項 e，と読むことができる．

さて，前編で導入した FA と PM という2つの意味計算規則を，この新しい言語に沿う形で再び埋め込む必要がある．

FA はHaskell における通常の関数適用として埋め込まれる．前編と同様に is_a という関数を定義しておく．

is_a :: a -> (a -> b) -> b
is_a x f = f x

また，PM は以下のように再定義される．

import Data.Extensible.Effect (Eff)

predicateModification
    :: (a -> Eff ctx Bool) -- ^ λx. p(x)
    -> (a -> Eff ctx Bool) -- ^ λx. q(x)
    -> (a -> Eff ctx Bool) -- ^ λx. p(x) ∧ q(x)
predicateModification p q = \x -> do
    p' <- p x
    q' <- q x
    pure $ p' && q'

また，前編で定義した $boy$ や $love$ といった語彙は以下のように再定義される．

boy :: PEANUTS -> Eff ctx Bool
boy x = pure $ case x of
    Charlie   -> True
    Linus     -> True
    Schroeder -> True
    _         -> False

love :: PEANUTS -> Eff ctx (PEANUTS -> Eff ctx Bool)
love object = do
    pure $ \subject -> pure $ case (subject, object) of
        (Lucy , Schroeder) -> True
        (Sally, Linus    ) -> True
        (Patty, Charlie  ) -> True
        _                  -> False

例として， ${\it \text{Snoopy is a cute dog.}}$ の意味計算は以下のように行われる．ただし cute および dog は前編で定義したものを適切に再定義したものとする．

sentence :: Eff '[] Bool
sentence = Snoopy `is_a` cuteDog
  where
    cute, dog, cuteDog :: PEANUTS -> Eff ctx Bool
    cute = _
    dog = _
    cuteDog = predicateModification cute dog

main :: IO ()
main = hspec $ do
    describe "Snoopy is a cute dog" $ do
        it "is false" $ do
            let denotation = leaveEff sentence
            denotation `shouldBe` False

ここで，leaveEff :: Eff '[] a -> a という関数が登場しているが，これは，文脈が空，すなわち ctx = '[] であるような場合にのみ，effectful な計算から中身を取り出すことのできる関数である．

§9のまとめ

変項割当を型安全に扱うために，以降は Eff ctx a という言語を用いる
- これは発話文脈 ctx を伴った a 型と読める

§10 Traces & Pronouns (T&P)

下準備が随分長くなってしまったが，いよいよ ${\it \text{She}_{\rm 1} \text{ loves } \text{him}_{\rm 2} \text{.}}$ という直示表現を含んだ文の意味計算を行うために，第3の意味計算規則である Traces & Pronouns (T&P) を導入する*7．

$\alpha_i$ が代名詞または痕跡で， $g$ が変項割当であり， $i$ が $g$ の定義域に含まれるとき， $[\![\alpha_i]\!] = g(i)$ である．

$\alpha _ i$ はそれ単体では意味が定まらないが，変項割当 $g$ によって指示対象が指定されているときに， $g$ を用いて意味計算を行なうことができる，ということを表している．ここでは例として

$g = \begin{equation} \left [ \begin{aligned} &1 \mapsto \text{Lucy} \\ &2 \mapsto \text{Schroeder} \\ \end{aligned} \right ] \end{equation}$

なる変項割当 $g$ のもとで ${\it \text{She}_{\rm 1} \text{ loves } \text{him}_{\rm 2} \text{.}}$ の意味計算を行ってみよう．

$\begin{align} [\![{\it{\text{She}_{\rm 1} \text{ loves } \text{him}_{\rm 2}}}]\!] &= [\![{\it \text{love him}_{\rm 2}}]\!]^g([\![{\it \text{she}_{\rm 1}}]\!]^g) & (\because \text{FA}) \\ &= [\![{\it \text{love}}]\!]^g([\![{\it \text{him}_{\rm 2}}]\!]^g)([\![{\it \text{she}_{\rm 1}}]\!]^g) & (\because \text{FA}) \\ &= (\lambda x y. y \text{ loves } x)([\![{\it \text{him}_{\rm 2}}]\!]^g)([\![{\it \text{she}_{\rm 1}}]\!]^g) & (\because \text{lexicon}) \\ &= (\lambda x y. y \text{ loves } x)(g(2))(g(1)) & \color{red}{(\because \text{T&P})} \\ &= (\lambda x y. y \text{ loves } x)(\text{Schroeder})(\text{Lucy}) & (\because \text{definition of } g) \\ &= (\lambda y. y \text{ loves Schroeder} )(\text{Lucy}) & (\because \beta \text{-reduction}) \\ &= \text{Lucy loves Schroeder} & (\because \beta \text{-reduction}) \\ &= \text{True} \end{align}$

さて，この T&P は Haskell では以下のように実装できる．ただし前述の通り，変項割当は値レベルではなく型レベルで表現する．

import Data.Kind (Type)
import Type.Membership (Assoc)

traceOrPronoun
    :: forall (index :: Nat) (entity :: Type) (ctx :: [Assoc Nat (Type -> Type)])
     . Lookup ctx index (ReaderEff entity)
    => Eff ctx entity
traceOrPronoun = askEff (Proxy @index)

ここで型変数 index :: Nat は，代名詞または痕跡に与えられた指標 (型レベル自然数) である．entity :: Type はその文において考えているモデルに存在する個体の型を表す型変数であり，具体的には PEANUTS 型などが代入される．ctx :: '[Assoc Nat (Type -> Type)] はこの発話がなされた発話文脈，すなわち変項割当である．また，Lookup ctx index (ReaderEff entity) という constraint は，この変項割当に対する要請を表している．どのような要請かというと，指標 index に対応する個体が定められていることを要求しているのである．

constraint を無視して => の後ろだけに注目すれば Eff ctx entity という単純な型をしており，(ctx という effects を伴った) 個体の型を表していることが見て取れる．また，実装部分は askEff Proxy と非常にシンプルで，ReaderEff entity という effect を発生させているだけであることがわかる．ただしこの effect は型レベル自然数 index に対応付けられている．

traceOrPronoun 関数を用いて ${\it \text{She}_{\rm 1} \text{ loves } \text{him}_{\rm 2} \text{.}}$ を Haskell に埋め込むと次のようになる．

import Data.Function ((&))

-- | "She(1) loves him(2)."
sentence :: Eff '[1 |-> PEANUTS, 2 |-> PEANUTS] Bool
sentence = do
    she      <- traceOrPronoun @1
    him      <- traceOrPronoun @2
    lovesHim <- love him
    she & lovesHim

このように組み立てた文の意味計算は runReaderEff 関数および前述の leaveEff 関数を用いて行う．

runReaderEff
    :: Eff ((index |-> PEANUTS) : ctx) a -- ^ ctx の先頭の @index |-> PEANUTS@ という effect を剥がす
    -> PEANUTS -- ^ 代わりに指標 index に対応する個体を外から与える
    -> Eff ctx a

実際に Haskell 上で意味計算を行う様子を以下に示す．

sentence :: Eff '[1 |-> PEANUTS, 2 |-> PEANUTS] Bool
sentence = do
    she1      <- traceOrPronoun @1
    him2      <- traceOrPronoun @2
    lovesHim2 <- love him2
    she1 & lovesHim2

main :: IO ()
main = hspec $ do
    describe "She(1) loves him(2)" $ do
        it "is true when she(1) refers Lucy and him(2) refers Schroeder" $ do
            let eval = leaveEff
                     . flip (runReaderEff @2) Schroeder
                     . flip (runReaderEff @1) Lucy
                denotation = eval sentence

            denotation `shouldBe` True

異なる変項割当のもとで意味計算を行った場合，その計算結果は当然違ったものになる．

        it "is false when she(1) refers Lucy and him(2) refers Charlie" $ do
            let eval = leaveEff
                     . flip (runReaderEff @2) Charlie
                     . flip (runReaderEff @1) Lucy
                denotation = eval sentence

            denotation `shouldBe` False

仮に不十分な発話文脈のもとで文が発話された場合，すなわち runReaderEff 関数で与えた変項割当が不十分である場合，コンパイルに成功しない．leaveEff :: Eff '[] a -> a 関数は ctx が空 ('[]) であることを要求するため，引数に effect が残存している場合には型が合わないためである．このように変項割当を型レベルで扱うことにより，発話文脈に対する型安全性を獲得することができる．

§10のまとめ

T&P という意味計算規則が導入された
- $\alpha_i$ が代名詞または痕跡で， $g$ が変項割当であり， $i$ が $g$ の定義域に含まれるとき， $[\![\alpha_i]\!] = g(i)$ である．
指標を型レベルで扱えば，T&P は askEff 関数によって表現でき，文脈上の具体的な指示対象は runReaderEff 関数によって与えられる

§11 Predicate Abstraction (PA)

関係代名詞を含んだ文の意味計算をしたい．以下に関係代名詞 ${\it \text{who}}$ を含んだ文の例を挙げる．

$\it{\text{The boy who Lucy loves t is a player.}}$

ただし $\it{\text t}$ は関係代名詞 $\it{\text who}$ が移動した痕跡 (trace) である．これらは指示対象としては同じものを指すので，同じ指標を与えることにする．

${\it \text{The boy } \text{who}_{\rm 1} \text{ Lucy loves } \text{t}_{\rm 1} \text{ is a player}.}$

また，player は Haskell 上で以下のように定義しておく．

player :: PEANUTS -> Eff ctx Bool
player x = pure $ case x of
    Snoopy    -> True
    Charlie   -> True
    Lucy      -> True
    Linus     -> True
    Patty     -> True
    Schroeder -> True
    _         -> False

さて，この文は次のような統語構造を持っている．

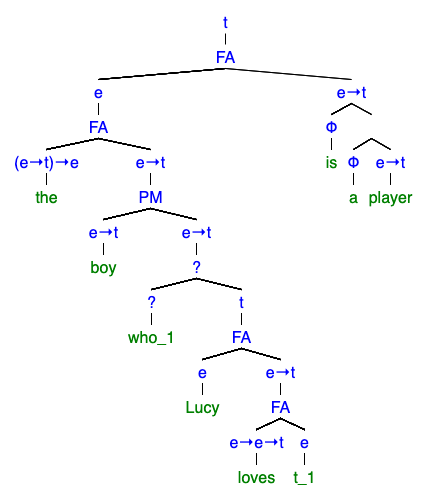
syntactic tree

principle of compositionality を根拠に，この構文木の部分木について考察することは有意義である．そこで，まずこの文の主部である $\it{\text{The boy } \text{who} _ {\rm 1} \text{ Lucy loves } \text{t} _ {\rm 1}}$ について考えてみよう．定冠詞 ${\it \text{the}}$ が付いていることから，この名詞節の意味はただ一つに定まる個体であることが予想される．つまり

${\it \text{The boy } \text{who} _{\rm 1} \text{ Lucy loves } \text{t} _ {\rm 1}} : e$

である．

この個体は発話文脈によらず一定である，すなわちこの名詞句は自由変項を含まない閉じた項になっている．構成要素に変項 $t _ {\rm 1}$ が含まれていることを考えると， $t _ {\rm 1}$ は頂点に至るまでのどこかで束縛されているはずである．部分木をボトム・アップに観察することによって，その様子を調べてみよう．

${\it \text{Lucy loves t} _ {\rm 1}}$

まず ${\it \text{Lucy loves t} _ {\rm 1}}$ という部分木を取り出すと，この部分の意味は既に知る通り FA と T&P によって計算することができる．ただし，この項の意味計算には指標 $1$ の指示対象を定める必要がある．この要請は Haskell の型において Lookup ctx 1 (ReaderEff PEANUTS) という形で現れる．

lucyLovesT1
    :: forall ctx
     . Lookup ctx 1 (ReaderEff PEANUTS)
    => Eff '[1 |-> PEANUTS] Bool
lucyLovesT1 = do
    t1      <- traceOrPronoun @1
    lovesT1 <- love t1
    Lucy & lovesT1

${\it \text{who} _{\rm 1} \text{ Lucy loves t} _ {\rm 1}}$

次に，関係代名詞節 ${\it \text{who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}}$ を見てみよう．この世の中の個体は，Lucy が愛するものとそうでないものに分類することができるので， $[\![{\it \text{who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}}]\!]$ は個体に関する述語である，つまり ${\it \text{who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}}$ は $e \to t$ 型をもつことが予想される． ${\it \text{loves}}$ の目的語である変項 ${\it{\text t}_{\rm 1}}$ に様々な個体を代入してみては，それを Lucy が愛してるか否かを検証する，といった具合である．

$[\![{\it \text{who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}}]\!]$ は純粋に個体に関する述語であり， ${\it \text{who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}}$ という項の意味は変項割当に依存しないという点に注目したい．部分木である ${\it \text{Lucy loves t} _ {\rm 1}}$ は意味計算にあたって $1$ の指示対象が定まっている必要があるにも関わらずである．

このような観察から，この ${\it \text{who}_{\rm 1}}$ が併合されるこの接点において， $t_{\rm 1}$ の部分が抽象化され， $\lambda x. \text{Lucy loves } x$ なる $D_e$ から $D_t$ への関数に変換されていることが見て取れる．実際のところ，このような意味計算はどのような規則に基づいて行われると解釈すべきであろうか．『形式意味論入門』4.4. に次のような言明がある．

すると，wh 句である ${\it \text{who} _ {\rm 1}}$ が行っている「仕事」は何だろうか．統語論的には， ${\it \text{who} _ {\rm 1}}$ は姉妹関係にある $t$ タイプの接点を $\langle e, t \rangle$ タイプに変換している．語彙的には，本来的には T&P によって $e$ タイプの個体として外延を導かれるはずの痕跡 $t_{\rm 1}$ を，変項に変換している．このふたつの操作を，同時に行うためには， ${\it \text{who} _ {\rm 1}}$ の外延を固定して設定し FA によって併合を行うよりも，新たな意味解釈規則を設定するほうが，汎用性が高い．そこで使われるのが PA という規則である．

つまり，関係代名詞 ${\it \text{who} _ {\rm 1}}$ は，「それ独自の外延をもたない」と考える．関係代名詞は，痕跡に割り振られている指標（index）と指示対象を同定する働きをしており，「単なる指標」として存在する．そして ${\it \text{who} _ {\rm 1}}$ の行っている「仕事」は，語彙項目によってではなく，PA によって遂行される．

というわけで，いささか天下り的だが，第4の意味計算規則である Predicate Abstraction を導入しよう．

Predicate Abstraction は以下のように定義される*8．

$\alpha$ が $\beta_{i}$ $(i \in \mathbb{N})$ および $\gamma$ を娘に持つ枝分かれ接点で， $\beta$ が代名詞または "such" であるとき，任意の変項割り当て $g$ のもとで $[\![\alpha]\!]^g = \lambda x \in D_e. [\![\gamma]\!]^{g[i \mapsto x]}$ となる．

ただし $g[i \mapsto x$ ] は modified variable assignment と呼ばれるもので，以下のように定義される*9．

$g$ を変項割当， $i \in \mathbb{N}$ ， $x \in D _ e$ とする．このとき， $g[i \mapsto x$ ] は以下の条件を満たす唯一の変項割当である．

(i) $dom(g[i \mapsto x]) = dom(g) \cup {i}$

(ii) $g[i \mapsto x](i) = x$

(iii) $j \neq i$ であるようなすべての $j \in dom(g[i \mapsto x])$ について $g[i \mapsto x](j) = g(j)$

ここで関数 $f$ に対し $dom(f)$ は $f$ の定義域を表す．

非形式的には，元となる変項割当 $g$ に対し， $i$ を与えたときに $x$ を返すように局所的な改変を加えて得られる新たな変項割当が $g[i \mapsto x$ ] であると言うことができる．

PA を用いて ${\it \text{who} _{\rm 1} \text{ Lucy loves } t _ {\rm 1}}$ の意味計算を行ってみよう．

$\begin{align} [\![{\it \text{who}_{\rm 1} \text{ Lucy loves } t _ {\rm 1}}]\!] &= \lambda x. [\![{\it \text{Lucy loves } t_{\rm 1}}]\!]^{\phi[1 \mapsto x]} & \color{red}{(\because \text{PA})} \\ &= \lambda x. [\![{\it \text{love}}]\!]^{\phi[1 \mapsto x]}([\![t_{\rm 1}]\!]^{\phi[1 \mapsto x]})([\![{\it \text{Lucy}}]\!]^{\phi[1 \mapsto x]}) & (\because \text{FA} \times 2) \\ &= \lambda x. (\lambda y z. z \text{ loves } y)([\![t_{\rm 1}]\!]^{\phi[1 \mapsto x]})(\text{Lucy}) & (\because \text{lexicon}) \\ &= \lambda x. (\lambda y z. z \text{ loves } y)(\phi[1 \mapsto x](1))(\text{Lucy}) & (\because \text{T&P}) \\ &= \lambda x. (\lambda y z. z \text{ loves } y)(x)(\text{Lucy}) & (\because \text{definition of } \phi[1 \mapsto x]) \\ &= \lambda x. (\lambda z. z \text{ loves } x)(\text{Lucy}) & (\because \beta \text{-reduction}) \\ &= \lambda x. \text{Lucy loves } x & (\because \beta \text{-reduction}) \end{align}$

PA を Haskell で実装すると以下のようになる．

predicateAbstraction
    :: forall index entity ctx a
     . Eff ((index |-> entity) ': ctx) entity
    -> Eff ((index |-> entity) ': ctx) a
    -> (entity -> Eff ctx a)
predicateAbstraction _ x = runReaderEff @index x

(index |-> entity) ': ctx という部分に着目してみると，改変前の ctx という変項割当に対し，index |-> entity という対応関係を cons して上書きしており，modified variable assignment を表現している．実装部分は単なる runReaderEff であり，まさにラムダ抽象を導入するというはたらきをしていることがわかる．

PA を用いた ${\it \text{who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}}$ の意味計算を Haskell 上で行うと以下のようになる．

-- | 与えられた個体は Lucy によって愛されているか？
whoLucyLoves :: Eff ('[] :: [Assoc Nat (Type -> Type)]) (PEANUTS -> Bool)
whoLucyLoves = predicateAbstraction @1 who1 lucyLovesT1
  where
    who1 :: forall ctx. Lookup ctx 1 (ReaderEff PEANUTS) => Eff ctx PEANUTS
    who1 = traceOrPronoun
    lucyLovesT1 :: forall ctx. Lookup ctx 1 (ReaderEff PEANUTS) => Eff ctx Bool
    lucyLovesT1 = _

effect の list が空 ('[]) になっており，もはや発話文脈に対して何の制約も課されてていないことがわかる．

${\it \text{boy who} _{\rm 1} \text{ Lucy loves } t _ {\rm 1}}$

${\it \text{boy}} : e \to t$ および ${\it \text{who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}} : e \to t$ について，どちらも外延は個体に関する述語であるから，この部分木の意味計算は PM によって行う．

$\begin{align} [\![{\it \text{boy who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}}]\!] &= \lambda x. [\![{\it \text{boy}}]\!](x) \land [\![{\it \text{who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}}]\!](x) & (\because \text{PM}) \\ &= \lambda x. x \text{ is a boy and Lucy loves } x \end{align}$

-- | 与えられた個体は，少年であり，かつ Lucy によって愛されているか？
boyWhoLucyLoves :: Eff '[] (PEANUTS -> Bool)
boyWhoLucyLoves = predicateModification boy whoLucyLoves
  where
    boy, whoLucyLoves :: Eff '[] (PEANUTS -> Bool)
    boy = _
    whoLucyLoves = _

${\it \text{the boy who} _{\rm 1} \text{ Lucy loves } t _ {\rm 1}}$

定冠詞 $the$ の外延 $[\![{\it \text{the}}]\!]$ はどのようなものだろうか．Heim and Kratzer では以下のように定義されている*10．

$f(x) = \text{True}$ となるような $x$ がちょうど1つだけ存在するような任意の関数 $f \in D_{e \to t}$ について， $[\![{\it \text{the}}]\!](f)$ は， $f(x) = \text{True}$ を満たすような唯一の $x$ である．

与えられた述語 $\phi$ を満たすような個体が，考えているモデル内にただ一つだけ存在するとき，その個体を ${\it \text{the }} \phi$ の意味とする．Model PEANUTS における語彙の定義に立ち返ると， $\lambda x. [\![{\it \text{boy who} _ {\rm 1} \text{ Lucy loves } t _ {\rm 1}}]\!](x)$ を $\text{True}$ にする個体 $x$ は $\text{Schroeder}$ のみなので， $[\![{\it \text{the boy who}_{\rm 1} \text{ Lucy loves } t_{\rm 1}}]\!] = \text{Schroeder}$ となるはずである．

Haskell では以下のように実装できる*11．モデル内の個体を列挙する必要があるため，Bounded entity および Enum entity という制約を追加せざるを得ない．

the
    :: (Bounded entity, Enum entity)
    => (entity -> Eff ctx Bool)
    -> Eff ctx entity
the predicate = do
    xs <- filterM predicate [minBound..maxBound]
    case xs of
        [x] -> pure x
        _   -> error "multiple entities satisfy the given predicate"

主部 ${\it \text{the boy who} _{\rm 1} \text{ Lucy loves } t _ {\rm 1}}$ の外延が $\text{Schroeder}$ であることがわかったので，あとは FA によって $[\![{\it \text{player}}]\!](\text{Schroeder})$ を計算すれば，元の文の外延が $\text{True}$ であることがわかる．

sentence :: Eff ('[] :: [Assoc Nat (Type -> Type)]) Bool
sentence = do
    let boyWhoLucyLoves = predicateModification boy whoLucyLoves
    theBoyWhoLucyLoves <- the boyWhoLucyLoves
    theBoyWhoLucyLoves & player
  where
    who1 :: forall ctx. Lookup ctx 1 (ReaderEff PEANUTS) => Eff ctx PEANUTS
    who1 = traceOrPronoun @1
    lucyLovesT1 :: forall ctx. Lookup ctx 1 (ReaderEff PEANUTS) => Eff ctx Bool
    lucyLovesT1 = do
        t1      <- traceOrPronoun @1
        lovesT1 <- love t1
        Lucy & lovesT1
    whoLucyLoves :: PEANUTS -> Eff ('[] :: [Assoc Nat (Type -> Type)]) Bool
    whoLucyLoves = predicateAbstraction @1 who1 lucyLovesT1

main :: IO ()
main = hspec $ do
    describe "The boy who(1) Lucy loves t(1) is a player" $ do

        it "is true" $ do
            let denotation = leaveEff sentence
            denotation `shouldBe` True

§11のまとめ

PA という意味計算規則が導入された
- $\alpha$ が $\beta_{i}$ $(i \in \mathbb{N})$ および $\gamma$ を娘に持つ枝分かれ接点で， $\beta$ が代名詞または "such" であるとき，任意の変項割り当て $g$ のもとで $[\![\alpha]\!]^g = \lambda x \in D_e. [\![\gamma]\!]^{g[i \mapsto x]}$ となる．
PA は runReaderEff 関数で表現できる

終わりに

本記事では『形式意味論入門』で紹介されている4つの意味計算規則を，その前提知識を交えて紹介し，Haskell のプログラムに書き下すことで理解を深めた．また，後半の2つの意味計算規則については，Haskell 上で型レベルの制約を表現することで，発話文脈に関する型安全性を獲得することができた．

本記事では筆者の見切り発車と技術的な制約により Haskell を採用したが，Haskell では副作用を扱うにあたってモナドを明示的にユーザに見せるという点であまり良い選択肢ではなかったかもしれない．後編の内容に関して言えば，暗黙に Kleisli 圏の上で考えるような，algebraic effects and handlers をネイティヴに扱える言語の方が向いているかもしれないので，機会があれば挑戦してみたい．

『形式意味論入門』では専ら外延意味論が取り上げられているが，外延意味論では「 $A$ は $p$ だと考えている」といった形式の，人間の信念に関する文を解釈することが難しい．このような問題に対するアプローチとして，内包意味論という枠組みが知られている．また，モデル論的意味論は，Tarski による数学の意味論に端を発するが，これに代わるものとして，証明論的意味論という意味論も展開されている．これは Gerhard Gentzen*12 や Dag Prawitz*13 らの数学の意味論を起源とし，Prawitz や Michael Dummett *14 による，文の意味を検証条件とする立場を嚆矢とするものである．

「形式意味論の特徴はラムダ演算子である」という触れ込みだったが，実際に意味論の世界で用いられているのは標準的な集合論であり，ラムダ抽象および適用の記法の使い勝手がよいので広く用いられている，というのが実態であるように感じられた (Montague による原典にあたればまた印象が変わるのかもしれない)．一方で，ラムダ計算の計算的側面に着目し，計算機の文脈で知られる概念を輸入したり，型システムを拡充したりすることによって，有益な示唆が得られたり，実際にモデルの説明力が向上するかもしれない．例としては，量化やフォーカスといったいくつかの言語現象が，継続の概念を用いてうまく説明できることが報告されている*15．他には依存型を用いると照応がうまく表現できると耳にしたことがある．また，Lambek 計算およびコンビネータ論理に立脚した組み合わせ範疇文法 (CCG; combinatory categorial grammar) も近年注目を集めているらしく，こちらも今後調べてみたい．

コード全文

{-# LANGUAGE AllowAmbiguousTypes #-}
{-# LANGUAGE DataKinds #-}
{-# LANGUAGE ExplicitNamespaces #-}
{-# LANGUAGE FlexibleContexts #-}
{-# LANGUAGE KindSignatures #-}
{-# LANGUAGE PackageImports #-}
{-# LANGUAGE PolyKinds #-}
{-# LANGUAGE ScopedTypeVariables #-}
{-# LANGUAGE StandaloneKindSignatures #-}
{-# LANGUAGE TypeApplications #-}
{-# LANGUAGE TypeOperators #-}

module Main where

import "base" Control.Monad (filterM)
import "base" Data.Function ((&))
import "base" Data.Kind (Type)
import "base" Data.Proxy (Proxy (Proxy))
import "base" GHC.TypeNats (Nat)
import "extensible-skeleton" Data.Extensible.Effect (askEff, Eff, leaveEff, ReaderEff, runReaderEff)
import "hspec" Test.Hspec (describe, hspec, it, shouldBe)
import "membership" Type.Membership (type (>:), Assoc, Lookup)

data PEANUTS
    = Snoopy
    | Woodstock
    | Charlie
    | Sally
    | Lucy
    | Linus
    | Patty
    | Schroeder
    deriving (Bounded, Enum)

type (|->) :: Nat -> entity -> Assoc Nat (Type -> Type)
type (index :: Nat) |-> entity = index >: ReaderEff entity

boy :: PEANUTS -> Eff ctx Bool
boy x = pure $ case x of
    Charlie   -> True
    Linus     -> True
    Schroeder -> True
    _         -> False

love :: PEANUTS -> Eff ctx (PEANUTS -> Eff ctx Bool)
love object = do
    pure $ \subject -> pure $ case (subject, object) of
        (Lucy , Schroeder) -> True
        (Sally, Linus    ) -> True
        (Patty, Charlie  ) -> True
        _                  -> False

cute :: PEANUTS -> Eff ctx Bool
cute x = pure $ case x of
    Lucy  -> True
    Patty -> True
    Sally -> True
    _     -> False

dog :: PEANUTS -> Eff ctx Bool
dog x = pure $ case x of
    Snoopy -> True
    _      -> False

player :: PEANUTS -> Eff ctx Bool
player x = pure $ case x of
    Snoopy    -> True
    Charlie   -> True
    Lucy      -> True
    Linus     -> True
    Patty     -> True
    Schroeder -> True
    _         -> False

is_a :: a -> (a -> b) -> b
is_a x f = f x

the
    :: (Bounded entity, Enum entity)
    => (entity -> Eff ctx Bool)
    -> Eff ctx entity
the predicate = do
    xs <- filterM predicate [minBound..maxBound]
    case xs of
        [x] -> pure x
        _   -> error "multiple entities satisfy the given predicate"

predicateModification
    :: (a -> Eff ctx Bool)
    -> (a -> Eff ctx Bool)
    -> (a -> Eff ctx Bool)
predicateModification p q = \x -> do
    p' <- p x
    q' <- q x
    pure $ p' && q'

traceOrPronoun
    :: forall (index :: Nat)
     . forall (entity :: Type)
     . forall (ctx :: [Assoc Nat (Type -> Type)])
     . Lookup ctx index (ReaderEff entity)
    => Eff ctx entity
traceOrPronoun = askEff (Proxy @index)

predicateAbstraction
    :: forall index entity ctx a
     . Eff ((index |-> entity) ': ctx) entity
    -> Eff ((index |-> entity) ': ctx) a
    -> (entity -> Eff ctx a)
predicateAbstraction _ x = runReaderEff @index x

main :: IO ()
main = hspec $ do
    describe "Snoopy is a cute dog" $ do
        let cuteDog = predicateModification cute dog
            sentence = Snoopy `is_a` cuteDog

        it "is true" $ do
            let denotation = leaveEff sentence
            denotation `shouldBe` False

    describe "She(1) loves him(2)" $ do
        let sentence :: Eff '[1 |-> PEANUTS, 2 |-> PEANUTS] Bool
            sentence = do
                she      <- traceOrPronoun @1
                him      <- traceOrPronoun @2
                lovesHim <- love him
                she & lovesHim

        it "is true when she(1) refers Lucy and him(2) refers Schroeder" $ do
            let eval = leaveEff
                     . flip (runReaderEff @2) Schroeder
                     . flip (runReaderEff @1) Lucy
                denotation = eval sentence

            denotation `shouldBe` True

        it "is false when she(1) refers Lucy and him(2) refers Charlie" $ do
            let eval = leaveEff
                     . flip (runReaderEff @2) Charlie
                     . flip (runReaderEff @1) Lucy
                denotation = eval sentence

            denotation `shouldBe` False

    describe "The boy who(1) Lucy loves t(1) is a player" $ do
        let whoLucyLoves :: PEANUTS -> Eff ('[] :: [Assoc Nat (Type -> Type)]) Bool
            whoLucyLoves =
                let who1 :: Lookup ctx 1 (ReaderEff PEANUTS) => Eff ctx PEANUTS
                    who1 = traceOrPronoun @1
                    lucyLovesT1 :: Lookup ctx 1 (ReaderEff PEANUTS) => Eff ctx Bool
                    lucyLovesT1 = do
                        t1 <- traceOrPronoun @1
                        lovesT1 <- love t1
                        Lucy & lovesT1
                 in predicateAbstraction @1 who1 lucyLovesT1
            sentence = do
                let boyWhoLucyLoves = predicateModification boy whoLucyLoves
                theBoyWhoLucyLoves <- the boyWhoLucyLoves
                theBoyWhoLucyLoves `is_a` player

        it "is true" $ do
            let denotation = leaveEff sentence
            denotation `shouldBe` True